再探龍博士圓盤拼片 (1)

過年比較沒時間認真寫東西，就來放個也是大部份寫好了一陣子的東西好了。這個大概是一年多前開始整理的，不過因為當時是寫在 Dropbox Paper 上，LaTeX 支援不足造成排版結果不甚滿意所以就沒放出來了；現在有了這個地方就來把它用好一點的 LaTeX 支援重新整理一遍。

2010 年底的時候，由於 puzzle 版的討論讓我簡單探索了龍博士圓盤拼片的結構，這方面最後的結論可以參照帕索當年總結我們的討論所寫下來的 blog 文章 (雖然當中一些圖已經由於帕索使用的圖床關係而失連了……)。

不過最近，由於一些原因，我想要重新計算龍博士圓盤的各個拼片的詳細尺寸，因此想說乾脆就把所有的計算和推導過程做個紀錄下來，順便把當年的挑戰題：所有 14 片拼片的面積來給出一個精確答案。

這系列預計一共會有三篇，都會歸在這個標籤下面；大致上的構成預計是：

(這一篇) 整理基本資料和容易計算的拼片面積
2-5 組合的探討
11-12-13 組合的探討

拼片整理和基本計算

拼片的基本資料已經整理在當年這三篇文章裡了：

其中第一篇是帕索的初步測量，後兩篇則是我的嘗試計算。全部 14 片的拼片當中， 2-5 和 11-12-13 這兩組有一些比較特殊的組合，這個留到後兩篇文章再來詳細探討；先針對其他的九片：1、3、4、6、7、8、9、10、14 號來做一些計算。以下假設整個圓盤 (以及所有弧長) 都是半徑為 1 的圓或弧，也就是整個圓的面積即為 $\pi$。

弧和弦的長度

可以看到，這九片的弧長一共有四種長度，若同樣依文中的方式以 $\frac1{12}$ 圓周長 ($\frac\pi6$弧度，$30\degree$) 為單位來描述的話，這四種長度分別是 1 單位、2單位、3單位、和一個稍微特別的「1.5」單位。這些弧長對應的弦長分別是：1 單位弧的弦長 $\frac12(\sqrt6-\sqrt2)$、2 單位弧的弦長 1、3 單位弧的弦長 $\sqrt2$、「1.5」單位弧的弦長則是 $\sqrt3-1$。稍微計算一下可以得知這個弧並不是正好 1.5 單位 ($\frac18$ 圓周長)：

$\frac18$圓弧對應的弦長為 $2\sin\frac\pi8=\sqrt{2-\sqrt2}\approx0.765$，比$\sqrt3-1\approx0.732$稍長；
反過來求弦長$\sqrt3-1$的圓心角為$2\arcsin(\frac12(\sqrt3-1))=\arccos(\sqrt3-1)\approx1.43138\times\frac\pi6$；這個 1.43138 即是我在第二篇文裡提到的數值。

不過以下行文為求方便，仍然將這個弧寫成帶引號的「1.5」單位。

這個弧乍看之下好像特立獨行，但接下來的計算會給出一兩個為何會是它的一種解釋。比起這個弧，後兩篇計算的 2-5 之間的弧以及 11 號葉子的弧才真的是特立獨行，其他的拼片都沒有這個弧。

弓形面積

講到弧，在計算拼片面積時有一類區域的面積很重要：由一弦和此弦的弧構成的弓形面積。
若將這弦／弧對應的圓心角記為 $\theta$，則弓形面積公式可由扇形面積減去三角形面積得到：$$\seg(\theta)=\frac12(\theta-\sin\theta)$$
上述的四個弧對應的弓形面積即為：

1 單位 $(\theta=\frac\pi6)$：$\seg(\frac\pi6)=\frac\pi{12}-\frac14$
2 單位 $(\theta=\frac\pi3)$：$\seg(\frac\pi3)=\frac\pi6-\frac{\sqrt3}4$
3 單位 $(\theta=\frac\pi2)$：$\seg(\frac\pi2)=\frac\pi4-\frac12$
「1.5」單位 $(\theta=\theta_s=\arccos(\sqrt3-1))$：$\seg(\arccos(\sqrt3-1))=\frac12(\arccos(\sqrt3-1)-\sqrt{2\sqrt3-3})$

「1.5」單位的角度 $\theta_s=\arccos(\sqrt3-1)$ 和其正弦值： $$\begin{alignat}{1}K_s&=\sin(\arccos(\sqrt3-1))\\&=\sqrt{1-(\sqrt3-1)^2}=\sqrt{2\sqrt3-3}\\&=\sqrt{\frac{\sqrt3}2(4-2\sqrt3)}=\frac12\sqrt{2\sqrt3}(\sqrt3-1)\end{alignat}$$ 這兩個數在後面的計算會一直出現，所以在此令為 $\theta_s$ 及 $K_s$。於是這個「1.5」單位的弓形面積即是 $\frac12(\theta_s-K_s)$。

拼片的基底三角形整理

回到這九片拼片。如果把拼片的弧所貼的基底三角形長度列出來的話，這九片一共可以分成五種大小：

2、2、3 單位弧：6、8 號
2、2、2 單位弧：14 號
1、「1.5」、2 單位弧：3、4、7、9 號
1、2、2 單位弧：1 號
「1.5」、3、3 單位弧：10 號

那麼以下就分別來計算。

6、8、14 號拼片

這三片是這九片當中比較簡單的。

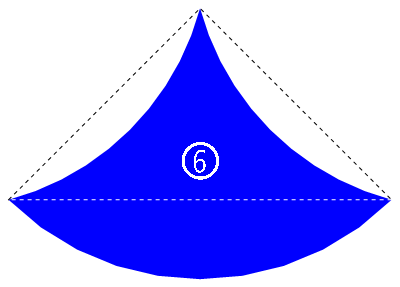
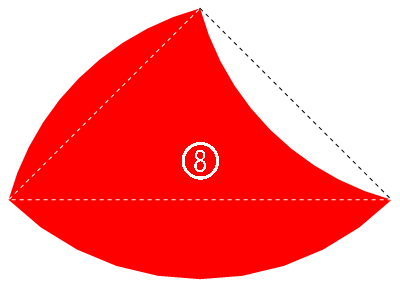
6、8 號的基底三角形其邊長是 1、1、$\sqrt2$，可以很明顯的看出是等腰直角三角形。這個三角形在 6 號上表現的很明顯，8 號由於兩個短弧一凸一凹的關係反而不那麼馬上看得出來；但也因為一凸一凹互相抵消，8 號的面積正好等於一個 $90\degree$ 扇形的面積，即 $A_8=\frac\pi4\approx0.785398$。6 號的面積我在上面第二篇文章已經說明過程了，結果是$A_6=\frac{\sqrt3}2-\frac\pi{12}\approx0.604226$。

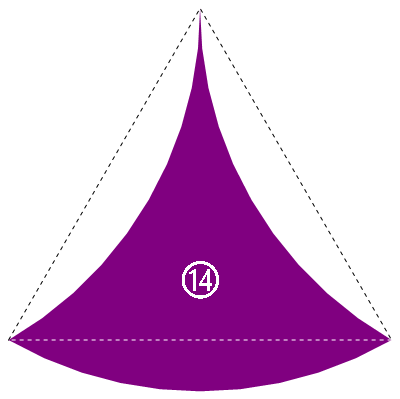
14 號的基底三角形是正三角形，邊長是 2 單位圓弧對應的弦長 1；但因為弓形是兩凹一凸，因此 14 號的面積是 $60\degree$ 扇形減去兩個 2 單位弓形面積，為 $A_{14}=\frac\pi6-2(\frac\pi6-\frac{\sqrt3}4)=\frac{\sqrt3}2-\frac\pi6\approx0.342427$。

3、4、7、9 號拼片

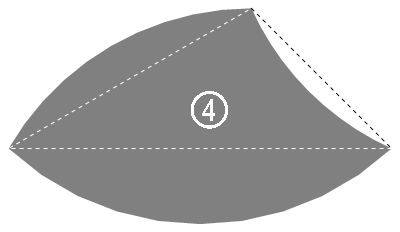
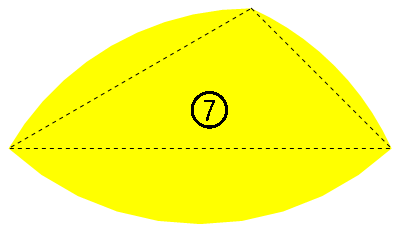
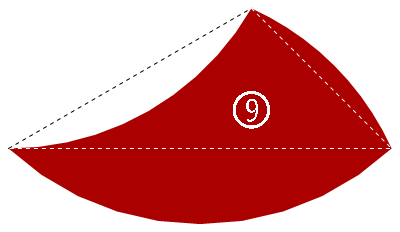
這四片的基底三角形其邊長是 $\frac12(\sqrt6-\sqrt2)$、$\sqrt3-1$、$1$。單純這樣看其實看不太出來是什麼比例，不過若同除以 $\frac{\sqrt3-1}2$ 的話，可以得到一個比較「簡單」的三邊比為 $\sqrt2:2:(\sqrt3+1)$。

為了進一步了解其形狀，以餘弦定理計算這三角形的角度大小：

$\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{2^2+(\sqrt3+1)^2-(\sqrt2)^2}{2\cdot2\cdot(\sqrt3+1)}=\frac{\sqrt3}2\Rightarrow A=\frac\pi6$
$\cos B=\frac{a^2+c^2-b^2}{2ac}=\frac{(\sqrt2)^2+(\sqrt3+1)^2-2^2}{2\cdot\sqrt2\cdot(\sqrt3+1)}=\frac{\sqrt2}2\Rightarrow B=\frac\pi4$

也就是說，這個三角形的角度是 $30\degree-45\degree-105\degree$這樣一個漂亮角度。這是其中一個 $\sqrt3-1$ 弦長出現的理由。
由求出的角度也能容易求出這三角形的面積：$\frac12\cdot(\sqrt3-1)\cdot1\cdot\sin\frac\pi6=\frac14(\sqrt3-1)$。

這四片的面積由此即可求得如下：

3 號拼片，2 單位弧凸，「1.5」單位弧和 1 單位弧都是凹，面積為$$\begin{alignat}{1}A_3&=\frac14(\sqrt3-1)+\left(\frac\pi6-\frac{\sqrt3}4\right)-\left(\frac\pi{12}-\frac14\right)-\frac12(\theta_s-K_s)\\&=\frac\pi{12}-\frac12(\theta_s-K_s)\approx0.22769\end{alignat}$$
4 號拼片，2 單位弧和「1.5」單位弧凸，1 單位弧是凹，面積為$$\begin{alignat}{1}A_4&=\frac14(\sqrt3-1)+\left(\frac\pi6-\frac{\sqrt3}4\right)-\left(\frac\pi{12}-\frac14\right)+\frac12(\theta_s-K_s)\\&=\frac\pi{12}+\frac12(\theta_s-K_s)\approx0.295909\end{alignat}$$
7 號拼片，三個弧都是凸，面積為$$\begin{alignat}{1}A_7&=\frac14(\sqrt3-1)+\left(\frac\pi6-\frac{\sqrt3}4\right)+\left(\frac\pi{12}-\frac14\right)+\frac12(\theta_s-K_s)\\&=\frac\pi4-\frac12+\frac12(\theta_s-K_s)\approx0.319508\end{alignat}$$
9 號拼片，2 單位弧和 1 單位弧凸，「1.5」單位弧凹，面積為$$\begin{alignat}{1}A_9&=\frac14(\sqrt3-1)+\left(\frac\pi6-\frac{\sqrt3}4\right)+\left(\frac\pi{12}-\frac14\right)-\frac12(\theta_s-K_s)\\&=\frac\pi4-\frac12-\frac12(\theta_s-K_s)\approx0.251289\end{alignat}$$

由 7、9 號拼片給出的 $\sqrt3-1$ 弦長

我在第二篇文章下面有提到我是怎麼找出這個 $\sqrt3-1$ 弦長的：是根據 7、9 號拼片可以拼成一個弧長 3 單位長的葉子形。下面就是這個葉子，其中我把兩片的基底三角形給標出來了：

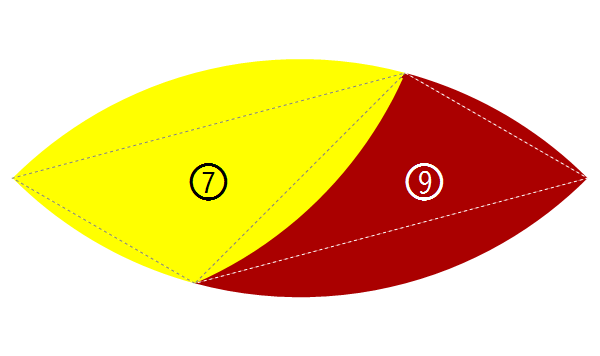
$\sqrt3-1$ 就是中間這一條斜線的長度。它是這麼求來的：
葉子的弧是 3 單位長 ($90\degree$)，所以它上面的圓周角對應 $270\degree$ 的弧，因此圓周角本身是 $135\degree$；圖中很容易看到一個平行四邊形，$135\degree$ 是它的一個角，因此其鄰角即是 $45\degree$；再由餘弦定理，已知夾此角的兩邊長是 1 和 $\frac12(\sqrt6-\sqrt2)$，即可求出第三邊長 $\sqrt3-1$。

雖然不知道發想如何，但這個 $30\degree$ 和 $45\degree$ 的設計應該是有意為之的－－這裡提供了一個 $45\degree$ 的好處，之後會提到另一個 $30\degree$ 能夠造成的效果。

1、10 號拼片

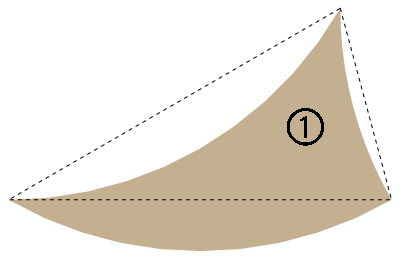
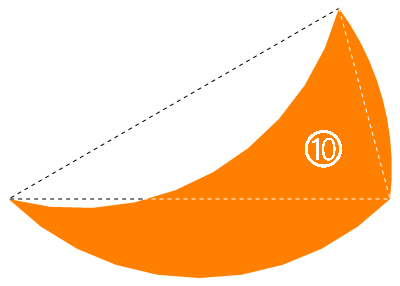
這兩片之所以會擺在一起講是因為它們的基底三角形其實是相似的等腰三角形：
1 號：10 號 = 2 單位弧的弦：3 單位弧的弦 (腰) = $1:\sqrt2$ = 1 單位弧的弦：「1.5」單位弧的弦 (底)。
後者比例是$1:\sqrt2$可以由上一節的比例得知；因此這裡是個 SSS 相似。

角度又如何呢？一樣由餘弦定理，等腰三角形的頂角為
$$\cos T=\frac{(\sqrt2)^2+(\sqrt2)^2-(\sqrt3-1)^2}{2\cdot\sqrt2\cdot\sqrt2}=\frac{\sqrt3}2\Rightarrow T=\frac\pi6$$ 是 $30\degree$角！於是底角也能推出是 $75\degree$。

10 號拼片看似跟 8 號一樣可以把長凸弧剪下來貼過去長凹弧，剩下一個 $30\degree$「扇形」¹；但是跟 8 號不同的是，剩下的凸弧是半徑 1 的弧，但等腰三角形的腰長 $\sqrt2$。所以這裡仍然要用三角形+弓形的方式計算。
三角形面積是$\frac12\cdot(\sqrt2)^2\cdot\sin\frac\pi6=\frac12$，加上弓形面積即為$A_{10}=\frac12+\frac12(\theta_s-K_s)\approx0.534109$。

1 號拼片狀況類似，長凸弧可以剪下來貼過去長凹弧²，但第三邊這次是凹弧。好在這裡的腰長又是 1 了，所以 1 號拼片的面積是 $30\degree$ 扇形減去兩個 1 單位弧的弓形：$A_1=\frac\pi{12}-2(\frac\pi{12}-\frac14)=\frac12-\frac\pi{12}\approx0.238201$。

以上重新計算了第三篇裡算過的九片的面積，這次這裡給出了精確式子，並驗證了那篇裡給出的近似值無誤。

下篇會來探討這組形影不離的 2、5 號拼片，以及上面提到過 7 號拼片裡的 $30\degree$ 能造成的另一個效果。

註腳

因為 10 號拼片較大，圖上可以看到大凹弧其實已經挖穿了三角形的另一邊了，這是因為這弧是 3 單位弧，圓心角 $90\degree$，故弦切角 $45\degree$ 大於頂角 $30\degree$ 的關係；不過這裡是拼補，有兩種看法可以解決：(1) 第一次補會凸一塊小弓形出來再補過去；或 (2) 先補再扣也可以。 ↩︎
1 號拼片的這弧是 2 單位弧，圓心角 $60\degree$，所以弦切角 $30\degree$ 等於頂角；可以看到三角形的另一邊確實切凹弧切在頂點。 ↩︎

拼片整理和基本計算

弧和弦的長度

弓形面積

拼片的基底三角形整理

6、8、14 號拼片

3、4、7、9 號拼片

由 7、9 號拼片給出的 \(\sqrt3-1\) 弦長

1、10 號拼片

註腳

發佈留言取消回覆

拼片整理和基本計算

弧和弦的長度

弓形面積

拼片的基底三角形整理

6、8、14 號拼片

3、4、7、9 號拼片

由 7、9 號拼片給出的 \(\sqrt3-1\) 弦長

1、10 號拼片

註腳

發佈留言 取消回覆

發佈留言取消回覆