這篇是系列文的第二篇,主要來探討 2-5 組合的詳細尺寸。其他系列文可由標籤連結。
4 單位的葉子
探討 2-5 這個特殊組合最好的方法還是跟著第三篇開頭提到的,從 2-5-1-7 這個 4 單位的葉子開始;同樣下圖我把這個組合當中的拼片基底三角形給畫出來了:
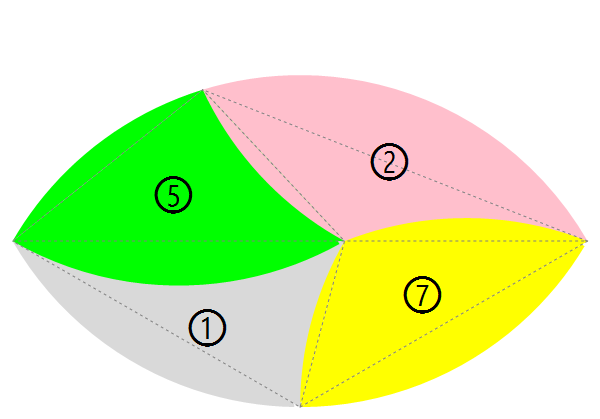
首先可以看到虛線部份有一條很直的直線,這條其實是這個葉子的中線。1 和 7 號拼片的 \(30\degree\) 在此發揮作用:由於兩拼片靠外的弧都是 2 單位 (\(60\degree\)),對應這弧的圓周角即是 \(30\degree\),由此即證明這兩個圓周角在此共線,這線就是葉子中線。這一點還能以兩邊交界的這一角進行驗證:7 號拼片的這角是 \(105\degree\),1 號拼片的底角是 \(75\degree\),湊起來正好是一個平角。
5 號拼片的圓周角和 2-5 之間的邊
對於我們有興趣的 2-5 ,這個平角的貢獻就在於它提供了一個計算切開 2-5 中間的這個弧的方法。5 號拼片靠外的弧是「1.5」單位弧,也就是它的弦長是 \(\sqrt3-1\);1 號和 5 號拼在一起的這條弧是 2 單位弧,即弦長為 1。關鍵點在於這個夾角,由於平角的關係,它正是對應 2 號拼片靠外的弧的圓周角;但這弧卻是 4 單位減去「1.5」單位,即 \(\frac{2\pi}3-\theta_s\)。這個角 (弧的一半) 的餘弦值為: $$\begin{alignat}{1}
\cos\theta_2&=\cos\left(\frac\pi3-\frac{\theta_s}2\right)
\\&=\cos\frac\pi3\cdot\cos\frac{\theta_s}2+\sin\frac\pi3\cdot\sin\frac{\theta_s}2
\\&=\frac12\cdot\sqrt\frac{1+\cos\theta_s}{2}+\frac{\sqrt3}2\cdot\sqrt\frac{1-\cos\theta_s}{2}
\\&=\frac12\sqrt\frac{\sqrt3}2+\frac{\sqrt3}2\sqrt\frac{2-\sqrt3}2
\\&=\frac{\sqrt{\sqrt3}}{2\sqrt2}+\frac{\sqrt3}2\cdot\frac{\sqrt3-1}2
\\&=\frac14(3-\sqrt3+\sqrt{2\sqrt3})
\end{alignat}$$ 然後由餘弦定理,這條 2-5 之間的弦長可以如此計算:$$\begin{alignat}{1}
c^2&=(\sqrt3-1)^2+1^2-2\cdot(\sqrt3-1)\cdot1\cdot\cos\theta_2
\\&=8-4\sqrt3-\frac12(\sqrt3-1)\sqrt{2\sqrt3}=8-4\sqrt3-K_s
\\c&=\sqrt{8-4\sqrt3-K_s}\approx0.624937
\end{alignat}$$ 其對應弧角為 \(\phi_{25}=2\arcsin\frac c2\),不過由於 \(c\) 的最外面是根號,這裡可以用倍角公式化簡:$$\begin{alignat}{1}
\sin^2\frac{\phi_{25}}2&=\left(\frac c2\right)^2=2-\sqrt3-\frac14K_s
\\\cos\phi_{25}&=1-2\sin^2\frac{\phi_{25}}2=1-(4-2\sqrt3-\frac12K_s)=-3+2\sqrt3+\frac12K_s
\\\phi_{25}&=\arccos\left(2\sqrt3-3+\frac12K_s\right)
\end{alignat}$$ 近似值為 \(\phi_{25}\approx1.21387\times\frac\pi6\)。這兩個數值即是之前第三篇中提到的計算結果。
5 號拼片的面積
那麼,這樣即可求出 5 號拼片的面積了;這個特殊夾角的正弦值以類似上法求得為:$$\begin{alignat}{1}
\sin\theta_2&=\sin\left(\frac\pi3-\frac{\theta_s}2\right)
\\&=\frac{\sqrt3}2\sqrt\frac{\sqrt3}2-\frac12\sqrt\frac{2-\sqrt3}2
\\&=\frac{\sqrt{3\sqrt3}}{2\sqrt2}-\frac12\cdot\frac{\sqrt3-1}2
\\&=\frac14\left(1-\sqrt3+\sqrt{6\sqrt3}\right)
\end{alignat}$$ 那麼三角形面積即為 $$\begin{alignat}{1}
\Delta_5&=\frac12\cdot(\sqrt3-1)\cdot1\cdot\frac14(1-\sqrt3+\sqrt{6\sqrt3})
\\&=\frac18(2\sqrt3-4)+\frac18(\sqrt3-1)\sqrt{6\sqrt3}
\\&=\frac{\sqrt3}4-\frac12+\frac14\sqrt3\cdot\frac12(\sqrt3-1)\sqrt{2\sqrt3}
\\&=\frac{\sqrt3}4-\frac12+\frac{\sqrt{3}}4K_s
\end{alignat}$$ 弓形面積方面,2 單位弓形面積 \(\frac\pi6-\frac{\sqrt3}4\) 和「1.5」單位弓形面積 \(\frac12(\theta_s-K_s)\)並不困難,但這條特殊邊的弓形面積就要算一下了:$$\begin{alignat}{1}
\sin\phi_{25}&=\sin\arccos\left(2\sqrt3-3+\frac12K_s\right)
\\&=\sqrt{1-\left(2\sqrt3-3+\frac12K_s\right)^2}
\\&=\sqrt{1-\left(21-12\sqrt3+(2\sqrt3-3)K_s+\frac12(2\sqrt3-3)\right)}
\\&=\sqrt{-\frac{77}4+\frac{23\sqrt3}2-(2\sqrt3-3)K_s}
\\&=\frac12\sqrt{-77+46\sqrt3-(8\sqrt3-12)K_s}
\\\textrm{seg}(\phi_{25})&=\frac12(\phi_{25}-\sin\phi_{25})
\\&=\frac12\phi_{25}-\frac14\sqrt{-77+46\sqrt3-(8\sqrt3-12)K_s}
\end{alignat}$$ 我們要求的 5 號面積就是 $$\begin{alignat}{1}
A_5&=\left(\frac{\sqrt3}4-\frac12+\frac{\sqrt{3}}4K_s\right)+\left(\frac\pi6-\frac{\sqrt3}4\right)+\frac12(\theta_s-K_s)
\\&-\left(\frac12\phi_{25}-\frac14\sqrt{-77+46\sqrt3-(8\sqrt3-12)K_s}\right)
\end{alignat}$$ 這當中只有 \(\frac{\sqrt3}4\)可以消掉,其他項長得完全不像所以都得留著。其近似值為\(A_5\approx0.33173\)。
2 號拼片的面積
2 號拼片現在有兩種算法:一是簡單的,由上面的葉子面積扣去已知的三片;另一是較繁的,求出 2 號拼片的外邊和圓周角再循上法求得面積。這裡打算兩者都做,先以較繁的做法求得結果,再以其求出葉子面積據以驗算。
圓周角和 5 號類似,只是這次對應的弧就是「1.5」單位弧本身,所以就是 \(\frac{\theta_s}2\),其正弦值上面求過是 \(\frac{\sqrt3-1}2\);外邊則為上面求過的此弧半角 (圓周角) 的正弦值 \(\sin\theta_2=\frac14(1-\sqrt3+\sqrt{6\sqrt3})\) 之兩倍。於是三角形面積為 $$\begin{alignat}{1}
\Delta_2&=\frac12\cdot(\sqrt3-1)\cdot\frac12(1-\sqrt3+\sqrt{6\sqrt3})\cdot\frac12(\sqrt3-1)
\\&=\frac18(10-6\sqrt3)+\frac18(\sqrt3-1)^2\sqrt{6\sqrt3}
\\&=\frac14(5-3\sqrt3)+\frac14(\sqrt3-1)\sqrt3\cdot\frac12(\sqrt3-1)\sqrt{2\sqrt3}
\\&=\frac14(5-3\sqrt3)+\frac14(3-\sqrt3)K_s
\end{alignat}$$ 外邊的弓形面積為 $$\begin{alignat}{1}
\seg(2\theta_2)&=\theta_2-\frac12\sin2\theta_2=\theta_2-\sin\theta_2\cos\theta_2
\\&=\frac\pi3-\frac{\theta_s}2-\left(\frac14(1-\sqrt3+\sqrt{6\sqrt3})\right)\left(\frac14(3-\sqrt3+\sqrt{2\sqrt3})\right)
\\&=\frac\pi3-\frac{\theta_s}2-\frac1{16}(1-\sqrt3+\sqrt{6\sqrt3})(3-\sqrt3+\sqrt{2\sqrt3})
\\&=\frac\pi3-\frac{\theta_s}2-\frac1{16}((1-\sqrt3)(3-\sqrt3)+((1-\sqrt3)+\sqrt3(3-\sqrt3))\sqrt{2\sqrt3}+\sqrt{6\sqrt3\cdot2\sqrt3})
\\&=\frac\pi3-\frac{\theta_s}2-\frac1{16}(6-4\sqrt3+(-2+2\sqrt3)\sqrt{2\sqrt3}+6)
\\&=\frac\pi3-\frac{\theta_s}2-\frac1{16}(12-4\sqrt3+4\cdot\frac12(\sqrt3-1)\sqrt{2\sqrt3})
\\&=\frac\pi3-\frac{\theta_s}2-\frac14(3-\sqrt3+K_s)
\end{alignat}$$ 於是最終 2 號拼片的面積為 $$\begin{alignat}{1}
A_2&=\left(\frac14(5-3\sqrt3)+\frac14(3-\sqrt3)K_s\right)+\left(\frac\pi3-\frac{\theta_s}2-\frac14(3-\sqrt3+K_s)\right)-\frac12(\theta_s-K_s)
\\&+\left(\frac12\phi_{25}-\frac14\sqrt{-77+46\sqrt3-(8\sqrt3-12)K_s}\right)
\\&=\frac12-\frac{\sqrt3}2+\left(1-\frac{\sqrt3}4\right)K_s+\frac\pi3-\theta_s+\frac12\phi_{25}-\frac14\sqrt{-77+46\sqrt3-(8\sqrt3-12)K_s}
\end{alignat}$$ 其近似值是\(A_2\approx0.338931\)。
這裡給的 \(A_2\) 和 \(A_5\) 的面積近似值也和我在第三篇文章裡給出的由 Mathematica 的公式所求出來的面積相同。
驗算
那麼就來進行上面提到的驗算了。首先先把 \(A_2+A_5\) 當中可以消的消掉。$$\begin{alignat}{1}
A_2+A_5&=\left(-\frac12+\frac{\sqrt3}4K_s+\frac\pi6+\frac12(\theta_s-K_s)-\seg(\phi_{25})\right)
\\&+\left(\frac12-\frac{\sqrt3}2+(1-\frac{\sqrt3}4)K_s+\frac\pi3-\theta_s+\seg(\phi_{25})\right)
\\&=\frac\pi2-\frac{\sqrt3}2-\frac12(\theta_s-K_s)
\end{alignat}$$另一方面,$$
A_1+A_7=\left(\frac12 – \frac\pi{12}\right)+\left(\frac\pi4-\frac12+\frac12(\theta_s-K_s)\right)
=\frac\pi6+\frac12(\theta_s-K_s)
$$ 於是\(A_2+A_5+A_1+A_7=-\frac{\sqrt3}2+\frac{2\pi}3\)。
而 4 單位弧的弓形面積是 \(\seg(\frac{2\pi}3)=\frac12(\frac{2\pi}3-\frac{\sqrt3}2)\),兩倍正好等於上行的面積和。驗算無誤。
下一篇要來挑戰大魔王,這組 11-12-13 的三片拼片了。之前的文章裡我只有給出近似測量,但這次就要認真來細算它們的尺寸了。