再探龍博士圓盤拼片 (3)

系列文的第三篇，來挑戰大魔王 11-12-13 組合了。前面兩篇文章可以由標籤連結。

從第五種困難度的一個答案開始

之所以會說是大魔王是因為，它們的長度組合其實是個很特定的數字，是建立在其他拼片的組合上切出來的。當年我用紙片湊出了一個第五種困難度的答案，從那裡才知道這三片拼片的實際大小。以下就是這組答案，同時將一些交點標上字母，下面有用：

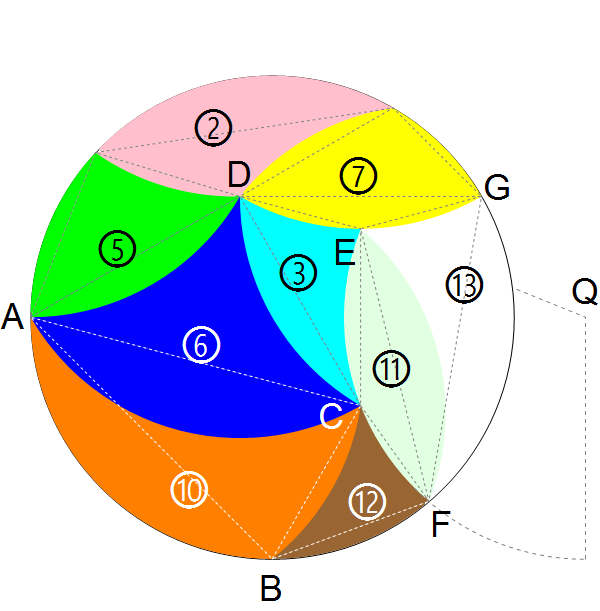
難度 5 的拼片除去還未知的 11、12、13，其他片的大小我們是已知的；而當它們拼成圖中這樣時，3 號拼片的「1.5」單位凹弧繼續延伸到盤邊就切出 12 號拼片，把這弧翻轉就能切出 11 號葉子拼片，13 號也就切出來了。但是這個弧長卻看似無法下手去求長度……

座標化

純幾何方法碰壁的話，只好用上一點暴力方法求解了：那就是座標化。如果能求出這個弧所在的圓應該就能求出長度了。

將這個圓盤擺到座標平面上。保持對稱，圓盤的圓心在原點非常合理；但座標軸方向要怎麼訂？這裡在邊邊的 10 號拼片給了我們方向：它的靠外弧是 3 單位弧 (\(90\degree\))！於是若將 10 號拼片的尖角放在 \(A(-1,0)\)，則它的鈍角就會在 \(B(0,-1)\)，接著就能由此求出所有交點的座標了。上圖只有把座標軸省略了，但是各片的位置是用這個座標畫出來的。接下來能求的座標依序是：

• 10 號拼片的第三點 \(C\)，這也是五個拼片所聚集的點。這裡可以由距離列聯立解，或是可以將 \(B\) 對 \(A\) 旋轉 \(30\degree\) 得到。無論如何，求得的座標是 \(C\left(\frac{\sqrt3-1}2,-\frac{\sqrt3-1}2\right)\)。
• 6 號拼片的尖點 \(D\)，一樣地可以由距離列聯立解，或是將原點 \(O\) 對 \(A\) 旋轉 \(30\degree\)¹，都可得到 \(D\left(\frac{\sqrt3}2-1,\frac12\right)\)。
• 3 號拼片的尖點 \(E\)，這個點沒有什麼可以轉的基準，所以只好列距離聯立解。解出來的座標是\(E\left(\frac{\sqrt3-1}2,\frac{\sqrt3-1}2\right)\)。

到這裡我們要的弧的端點 \(C\) 和 \(E\) 已經求出來了。幸運的是這兩個點的 \(x\) 座標相等，\(y\) 座標互為相反數，因此我們要的圓心座標的 \(y\) 座標一定是 0。\(x\) 座標則由畢氏定理可以求：\(\sqrt{1-(\frac{\sqrt3-1}2)^2}=\frac12\sqrt{2\sqrt3}\)，即 \(x\) 座標為\(\frac12(\sqrt3-1+\sqrt{2\sqrt3})\)。也就是說，我們要找的圓心在 \(Q(\frac12(\sqrt3-1+\sqrt{2\sqrt3}),0)\)！

這個求出來的 \(x\) 座標還有一個很有趣的特性：令它為 \(K_x\) 的話，它的平方是 $$\begin{alignat}{1}
K_x^2&=\frac14(4-2\sqrt3+2(\sqrt3-1)\sqrt{2\sqrt3}+2\sqrt3)
\\&=1+\frac12(\sqrt3-1)\sqrt{2\sqrt3}=1+K_s
\end{alignat}$$ 也就是我們其實有 \(K_x=\sqrt{1+K_s}\)。

有了圓心座標就能求兩個圓的交點了。圓 \(O\) 和圓 \(Q\) 的 \(y\) 座標相等，所以交點的 \(x\) 座標會和線段 \(\overline{OQ}\) 的中點的 \(x\) 座標相等，是 \(\frac12K_x\)。\(y\) 座標就再度使用畢氏定理求之：\(1-(\frac12K_x)^2=1-\frac14(1+K_s)=\frac34-\frac14K_s=\frac14(3-K_s)\) 。於是我們的交點座標即為 \(F(\frac12K_x,-\frac12\sqrt{3-K_s})\)。

以下再記\(K_y=\sqrt{3-K_s}=\sqrt{3-\sqrt{2\sqrt3-3}}\)，也就是 \(F\) 點座標就是\((\frac12K_x,-\frac12K_y)\)。這兩個值的形式上可以看到有 \(K_x^2+K_y^2=4\)，這和 \(F\) 點到原點 \(O\) 的長度為 1 吻合。

11 號拼片

交點算出來了，接下來要來求弧 \(\overarc{EF}\) 的弧角 \(\beta\)。
用的方法是向量內積，由圓心連向這兩個點的單位向量內積即是它們的夾角了：$$\begin{alignat}{1}
\vec{QE}&=\left(-\frac{\sqrt{2\sqrt3}}2,\frac{\sqrt3-1}2\right)
\\\vec{QF}&=\left(-\frac12K_x,-\frac12K_y\right)
\\\cos\beta&=\vec{QE}\cdot\vec{QF}
\\&=\frac{\sqrt{2\sqrt3}}2\cdot\frac12K_x-\frac{\sqrt3-1}2\cdot\frac12K_y
\\&=\frac{\sqrt{2\sqrt3}}2\cdot\frac14(\sqrt3-1+\sqrt{2\sqrt3})-\frac{\sqrt3-1}2\cdot\frac12K_y
\\&=\frac18\left((\sqrt3-1)\sqrt{2\sqrt3}+2\sqrt3\right)-\frac14(\sqrt3-1)K_y
\\&=\frac14K_s+\frac14\sqrt3-\frac14(\sqrt3-1)K_y
\\&=\frac14(K_s+\sqrt3-(\sqrt3-1)K_y)
\end{alignat}$$ 為了後續計算，先把這個角的正弦值也求出來。計算有一點繁所以直接上結果：
$$\begin{alignat}{1}
\cos^2\beta=-\frac12(\sqrt3-1)(K_s+\sqrt3)(K_y-2)
\\\sin^2\beta=1+\frac12(\sqrt3-1)(K_s+\sqrt3)(K_y-2)
\\\sin\beta=\sqrt{1+\frac12(\sqrt3-1)(K_s+\sqrt3)(K_y-2)}
\end{alignat}$$ 感覺不像是個有好表示式的東西。
這個弧角有多大呢？Mathematica 告訴我的近似值是 \(\beta\approx2.36853\times\frac\pi6\)。
11 號的面積用這個弧角表示很簡單：\(2\seg(\beta)=\beta-\sin\beta\)，但是代進去就是更大一團的消不掉的東西：$$
A_{11}=\beta-\sin\beta=\arccos\left(\frac14(K_s+\sqrt3-(\sqrt3-1)K_y)\right)-\sqrt{1+\frac12(\sqrt3-1)(K_s+\sqrt3)(K_y-2)}
$$ 近似值是 \(A_{11}\approx0.294325\)。

13 號拼片

接下來輪到 13 號拼片了；首先先求它的長弧角 \(\overarc{FG}=\alpha\)。\(G\) 點座標其實很好求：從在負 x 軸上的 \(A\) 點開始，經過 5-2-7 號的外圍到達 \(G\) 點。5-2 號弧長 4 單位，7 號這個邊是 1 單位，所以 \(G\) 點的幅角是水平起算正 1 單位，也就是座標是 \(G\left(\frac{\sqrt3}2,\frac12\right)\)。於是我們要求的 \(\alpha\) 即為 \(\frac\pi6\) 減去 \(F\) 的幅角 \(\arcsin(-\frac12K_y)\)－－同樣用倍角公式消掉 \(K_y\) 最外層的根號：$$\begin{alignat}{1}
\xi&=\arcsin(-\frac12K_y)\\
\sin^2\xi&=\frac14(3-K_s)\\
\cos2\xi&=1-2\sin^2\xi=\frac12(K_s-1)\\
\xi&=\pm\frac12\arccos\left(\frac12(K_s-1)\right) \mathtt{(正不合)}\\
\alpha&=\frac\pi6-\xi=\frac\pi6+\frac12\arccos\left(\frac12(K_s-1)\right)\approx2.65284\times\frac\pi6
\end{alignat}$$ 當年我的直接比較是說它跟 2 號拼片的「2.5」單位差不多，實際數字也確證這一點：2 號拼片的「2.5」單位實際上是 4 – 1.43138 = 2.56862單位弧，13 號拼片的長弧又稍微長一些些了。

接下來是面積。13 號拼片的三邊中，短邊是 1 單位弧，故弦長是 \(\frac12(\sqrt6-\sqrt2)\)；靠 11 的內弧是 \(\beta\) 角，弦長是 \(2\sin\frac\beta2\)；靠外的外弧是 \(\alpha\) 角，弦長是 \(2\sin\frac\alpha2\)。
先求 \(2\sin\frac\beta2\)，這個可以建立在上面求過的 \(\cos\beta\) 上：$$\begin{alignat}{1}
2\sin\frac\beta2&=2\sqrt{\frac{1-\cos\beta}2}\\
&=\sqrt{2-2\cos\beta}\\
&=\sqrt{2+\frac12(K_y^2+(\sqrt3-1)K_y-(3+\sqrt3))}\\
&=\sqrt{\frac12K_y^2+\frac{\sqrt3-1}2K_y+\frac12(1-\sqrt3)}\\
&=\sqrt{\frac12\left(K_y+\frac{\sqrt3-1}{2}\right)^2-\frac{\sqrt3}4}
\end{alignat}$$ \(2\sin\frac\alpha2\) 則一樣先求 \(\cos\alpha\)：$$\begin{alignat}{1}
\cos\alpha&=\cos\left(\frac\pi6+\arcsin\left(\frac12K_y\right)\right)\\
&=\frac{\sqrt3}2\cos\arcsin\left(\frac12K_y\right)-\frac12\sin\arcsin\left(\frac12K_y\right)\\
&=\frac{\sqrt3}2\sqrt{1-\left(\frac12K_y\right)^2}-\frac12\cdot\frac12K_y\\
&=\frac{\sqrt3}4\sqrt{4-K_y^2}-\frac14K_y\\
&=\frac{\sqrt3}4K_x-\frac14K_y\\
&=\frac14(\sqrt3K_x-K_y)\\
2\sin\frac\alpha2&=\sqrt{2-2\cos\alpha}\\
&=\sqrt{2-\frac{\sqrt3}2K_x+\frac12K_y}
\end{alignat}$$
從這裡要求出任何一個角度都是一個浩大的工程。不過眼尖的人可能看到了上圖 13 號拼片的基底三角形好像有個玄機……

那就是 \(\triangle EFG\) 好像是個直角三角形？！來實際計算看看吧：$$\begin{alignat}{1}
\overline{EG}^2+\overline{FG}^2&=\left(\frac12(\sqrt6-\sqrt2)\right)^2+\left(\sqrt{\frac12(K_y+\frac{\sqrt3-1}{2})^2-\frac{\sqrt3}4}\right)^2\\
&=(2-\sqrt3)+\left(\frac12\left(K_y+\frac{\sqrt3-1}{2}\right)^2-\frac{\sqrt3}4\right)\\
&=\frac12\left(K_y+\frac{\sqrt3-1}{2}\right)^2+2-\frac54\sqrt3\\
\overline{EF}^2&=\left(\sqrt{2-\frac{\sqrt3}2K_x+\frac12K_y}\right)^2\\
&=2-\frac{\sqrt3}2K_x+\frac12K_y
\end{alignat}$$……看起來不像相等。以 Mathematica 計算可知這兩個結果差了約 1.2%，所以那個角並不是直角，它大約是 \(90.94\degree\)。

既然沒有特殊角只好老老實實回到海龍公式來求面積－－或者因為這幾個邊長都有根號，用秦九韶公式或許會好算一點：在$$\triangle_{13}=\frac12\sqrt{a^2c^2-\left(\frac{a^2+c^2-b^2}2\right)^2}$$ 當中令 $$\begin{cases}
a^2=2-\frac{\sqrt3}2K_x+\frac12K_y\\
c^2=\frac12\left(K_y+\frac{\sqrt3-1}{2}\right)^2-\frac{\sqrt3}4\\
b^2=2-\sqrt3\end{cases}$$ 代入……然後就發現根號裡還是一大團。Mathematica 把 \(\triangle_{13}\) 化簡寫成根式之後是長這樣：

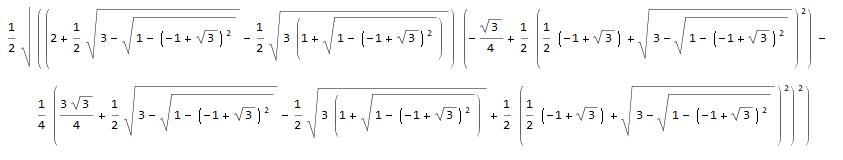
……就擺著好了。
如果算上弓形面積狀況並不會更好，因為除了短凹弧有短一點的式子 \(\frac\pi{12}-\frac14\) 之外，長凹弧 \(\frac12(\beta-\sin\beta)\) 和長凸弧 \(\frac12(\alpha-\sin\alpha)\) 都不是好算的東西，而且會跟 11 號拼片一樣會產生消不掉的反三角函數，所以就只能這樣列式出來表示了：$$A_{13}=\triangle_{13}-\left(\frac\pi{12}-\frac14\right)+\frac12\left(\alpha-\beta-\sin\alpha+\sin\beta\right)\approx0.344548$$

12 號的弧角和面積

最後是小塊的 12 號了。它和 10 號接觸的長凹弧是 10 號的短凸弧「1.5」單位，而有了之前求的 \(\alpha,\beta\) 角，另外兩個弧也可以寫出來：和 11 號接觸的小凹弧是 \(\beta-\arccos(\sqrt3-1)\approx0.937154\times\frac\pi6\)，和外圈接觸的凸弧是 \(\frac{2\pi}3-\alpha\approx1.34716\times\frac\pi6\)。當年我用紙片直接比較的結果是：凸「1.5」、凹 1、凹「1.5」，和實際數字確實差不多。

面積方面，這裡有一個不用再去求複雜弧長的方式：回到當年的第一篇文章，帕索在推文裡有問說：

→ puzzlez:那請問 11 -12 -13 可不可以拼出 8 ？

而我在第三篇文章裡這麼回答了：

拿紙切的拼片拼一拼後應該是 2,3,5,6,7,10,11,12,13²
帕索你問的 11~13 是不是能拼成 8 號應該是從這裡來的
因為 2,3,5,6,7,8,10³ 也可以拼起來…
不過如果能拼出 8 號我那題 10-3 就解開了
所以應該是不能拼但面積總和相等…

也就是說，\(A_{11}+A_{12}+A_{13}=A_8=\frac\pi4\)。詳細式子可以由上面計算結果套用而得所以這裡也不寫了，只給出面積近似值 \(A_{12}\approx0.146526\)。這和當年我給出來的 \(0.099865\) 之間的誤差就是在上面量的弧長的差別 ，尤其是長凸弧差了 10% 左右。

總整理和一個有趣的問題

至此所有拼片的面積都已經求出來了，這裡將全部 14 片的面積整理成表：

拼片	面積近似值 (全圓盤為 \(\pi\approx3.141593\))	面積佔全圓盤的比例
1	0.238201	7.5821%
2	0.338931	10.7885%
3	0.227690	7.2476%
4	0.295909	9.4191%
5	0.331730	10.5593%
6	0.604226	19.2331%
7	0.319508	10.1703%
8	0.785398	25%
9	0.251289	7.9988%
10	0.534109	17.0012%
11	0.294325	9.3687%
12	0.146526	4.6641%
13	0.344548	10.9673%
14	0.342427	10.8998%

最後，有了這個可以來回答一個有點有趣的問題：龍博士圓盤還有沒有其他的組合可能有解？

為此，這裡用另一種方式來整理這 14 片拼片的面積：

拼片	面積	\(\frac\pi{12}\)	\(\frac12\)	\(\frac{\sqrt3}2\)	\(\seg(\theta_s)\)
6	\(\frac{\sqrt3}2-\frac\pi{12}\)	-1	0	1	0
8	\(\frac\pi4\)	3	0	0	0
14	\(\frac{\sqrt3}2-\frac\pi6\)	-2	0	1	0
3	\(\frac\pi{12}-\seg(\theta_s)\)	1	0	0	-1
4	\(\frac\pi{12}+\seg(\theta_s)\)	1	0	0	1
7	\(\frac\pi4-\frac12+\seg(\theta_s)\)	3	-1	0	1
9	\(\frac\pi4-\frac12-\seg(\theta_s)\)	3	-1	0	-1
1	\(\frac12-\frac\pi{12}\)	-1	1	0	0
10	\(\frac12+\seg(\theta_s)\)	0	1	0	1
2+5	\(\frac\pi2-\frac{\sqrt3}2-\seg(\theta_s)\)	6	0	-1	-1
11+12+13	\(\frac\pi4\)	3	0	0	0

這張表的右邊可以提供湊面積的參考；所選的列最右邊三欄的值總和要為 0。若再依據 \(\frac\pi{12}\) 的數量分類的話，一共有以下組合：

• \(\frac2{12}\pi=\frac16\pi\)：(3,4)
• \(\frac3{12}\pi=\frac14\pi\)：(1,3,7)、(1,4,9)、(8)、(9,10)、(11,12,13)
• \(\frac5{12}\pi\)：(2,4,5,14)
• \(\frac6{12}\pi=\frac12\pi\)：(1,2,5,7,14)、(2,4,5,6)
• \(\frac7{12}\pi\)：(1,2,5,6,7)
• \(\frac8{12}\pi=\frac23\pi\)：(2,3,5,7,10,14)
• \(\frac9{12}\pi=\frac34\pi\)：(2,3,5,6,7,10)

上面的組合中可由小的組合湊出來的就略去，例如四分之三圓有一個 (1,2,3,4,5,6,7) 可以看成 (1,3,7) + (2,4,5,6) 或 (1,2,5,6,7) + (3,4) 的組合，因此不列入上表。
從這裡再去組合出整圓的組合共有 12 種，可以分成以下三類：

• {(1,2,5,7,14), (2,4,5,6)} + {(1,3,7), (8), (9,10), (11,12,13)}x2：半圓二選一加上四分之一圓四選二。扣掉重覆拼片的話共有九種組合：
  • (2,4,5,6) + (1,3,7) + (8)：第二種困難度
  • (2,4,5,6) + (1,3,7) + (9,10)：第一種困難度
  • (2,4,5,6) + (1,3,7) + (11,12,13)：第八種困難度⁴
  • (2,4,5,6) + (8) + (9,10)：第六種困難度
  • (2,4,5,6) + (8) + (11,12,13)：???
  • (2,4,5,6) + (9,10) + (11,12,13)：???
  • (1,2,5,7,14) + (8) + (9,10)：第三種困難度
  • (1,2,5,7,14) + (8) + (11,12,13)：???
  • (1,2,5,7,14) + (9,10) + (11,12,13)：第九種困難度
• (2,3,5,6,7,10) + {(8), (11,12,13)}：四分之三圓加上四分之一圓二選一。這分別是：
  • (2,3,5,6,7,10) + (8)：第四種困難度
  • (2,3,5,6,7,10) + (11,12,13)：第五種困難度
• (1,3,7) + (8) + (9,10) + (11,12,13)：四個四分之一圓全選。這是第七種困難度。

由於拼片設計的關係，雖然存在能夠組成面積對的答案但並不能直接肯定有沒有解；不然當年那個無解題就不會無解了 (苦笑)。所以剩下的三個組合 (2,4,5,6,8,11,12,13)、(2,4,5,6,9,10,11,12,13)、(1,2,5,7,8,11,12,13,14) 究竟有沒有解可能也要多方嘗試才能知道了。

那麼這就是對當年的挑戰題：全部十四片拼片的面積的詳細解答。

註腳

1. 理由是：首先 \(\overline{AD}\) 是 6 號拼片的腰，長度為 1；其斜率可自 \(\overline{AB}\) 斜率 \(-45\degree\) 起算，加上 10 號拼片的頂角 \(\angle BAC = 30\degree\)，加上 6 號拼片的底角 \(\angle CAD = 45\degree\)，總計是 \(+30\degree\)。 ↩︎
2. 這就是這篇開頭提到的第五種困難度。 ↩︎
3. 這是第四種困難度。 ↩︎
4. 七八九這三種困難度的資料是來自 playertsai 的文章。 ↩︎