#184 Triangles containing the origin (難度 75%)
這題題目描述起來很簡單:考慮平面上一些點的集合,這些點滿足:點的座標為整數,以及它們都在一個圓心在原點,半徑為 r 的圓的內部。考慮由這點集當中的點為頂點的三角形,計算圓心 (原點) 在其內部的三角形個數。
對 r=2,一共可以找得到 8 個原點在內部的三角形;r=3 有 360 個,而 r=5 則有 10600 個。試求 r=105 時有多少個。
看起來很簡單,但仔細想下去就會發現很多細節藏在裡面:
- 首先,點的數量很多:用圓面積估計可以得到半徑 105 的圓內整點數約有三萬四千多個,在其中選三個的選法有近七兆種;
- 三角形要包含圓心。說起來簡單,但包含這回事並不容易化成條件;
- 看起來好像有一些對稱性可以用,但這又不是大家都一樣的對稱 (有的翻轉不同,有的翻轉相同等等),要分狀況會很麻煩;
- 等等。
先來提「包含」這件事好了;因為這題其實是個標準的計算幾何題目。所謂計算幾何,以不那麼精準的懶人包說法就是:把幾何問題座標化的解析算式用電腦程式計算的演算法。畢竟電腦要「看」一個幾何圖形只能用描述它的參數性質去看,一些只要圖畫出來對人來說很直接的判斷,電腦程式都需要進行一些運算才能判定;加上一些幾何上的簡單性質其實很容易出現無理數 (以最常見的直角三角形來說好了,畢氏定理求斜邊會有根號,而角度則就連有理數度都是少數),若沒有特別設計的話數值精確度也會是一個問題。
在計算幾何當中要求一個點是否包在簡單多邊形當中,常用的做法有幾個:
- 繞多邊形的邊,每次都看該點是否在邊的同一側:想像沿著多邊形開車,結果繞了一圈都發現目標點都在同一邊,那就可以知道這個點在多邊形裡面了。從這個形象化也很容易知道知道這個方法只對凸多邊形有用,不過三角形一定是凸的所以對三角形也算常用。
- 從點任意發射射線,如果只和多邊形交叉奇數次那就是在裡面:這也是個在圖形上滿直觀的做法。
- 上一個方法的進階版:計算這個多邊形對所求點的卷繞數,如果不是零那就是在裡面。
等等。
單單只運用這些方式就能輕鬆寫程式檢驗題目給的三個數字,但直上 r=105 時就會卡住了。這才是這題的困難點:點集內有 \(O(r^2)\) 個點,所以選三個點組成的三角形個數有 \(O(r^6)\) 個,全部試過一遍的時間會太久。

上面第三個方法提到的卷繞數,仔細思考可以發現對於多邊形其實可以進行簡化:因為多邊形的邊是直線,沿著邊繞時我們可以由起點和終點的方向知道這邊會增加或減少卷繞數;而若包這一點的是簡單多邊形,卷繞數只會是 1 或 -1 (看是繞哪個方向),因此對於三角形就可以簡化成:每個邊繞的方向都一樣的話它就會包住原點。
既然我們只要全部相同的方向的話,那不如我們自己取,這樣還可以省去判斷;只要找一個取法能夠把所有該算得到的三角形都算到就行了。既然上面的簡化版是由頂點到頂點這樣掃,那我們可以先把所有可能的頂點所在方向算出來,那由一個點掃到另一個點就只要看這兩個點的方向就能判斷這一掃是正向還是反向。這樣一來,隨便取兩個點,第三個點的所在方向是有限定的:例如下圖,只有在著色區域當中的 C 點才能和 A B 合成包含 O 點的三角形。
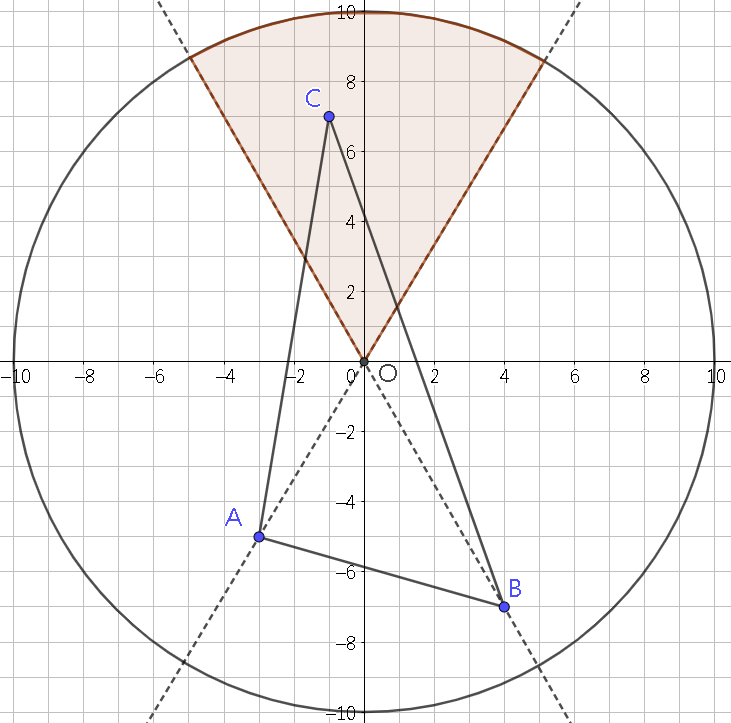
思考到這邊,我們的演算法就很清楚了:
- 枚舉所有的 A 和 B 的組合。A 可以只限定在一個半圓,因為要包含原點任何一個半圓至少會有一個點;
- 對每個組合,使用上面的方式找出可以用的 C 點範圍,把這範圍內的 C 點個數加進計算。
因為 C 點範圍可以讓 A 和 B 決定,所以第一個枚舉的項數減少到 \(O(r^4)\) 了。為了要能快速求出上面這樣的範圍,我們可以把所有點依照方向排序,那只要 A B 取定了之後很容易就能找到對面方向在哪裡,就能簡單的求出範圍內點數,加總起來就是所需要的答案了。
……只要你的程式沒有因為數值精確度而漏算多算的話。
是的,這題的難關其實不是演算法,而是當你直接用數學關係寫程式時會遇上的數值精確度問題。
問題是在將點依方向排序上。排序不是問題,但這個「方向」,有一點三角函數底子的人應該會直覺想到 atan (反正切) 函數從斜率求角度,比較有注意到細節的人可能還會使用會考慮進象限的 atan2 來求方向;問題在於,因為我們有的是整數點,反正切函數幾乎不會出現有理數結果 (整數點只有正 x 方向的點的反正切值 0 是有理數而已),這樣一來同一個方向的結果有可能會有不同精確度的答案。因為這個關係,要怎麼決定一個方向的對面從哪裡開始也會是個問題:180 度是 \(\pi\) 弧,而 \(\pi\) 是無理數,已知方向的角也是無理數,要確定加 \(\pi\) 的角度附近哪些也是一樣的角度有點麻煩。這就是造成上面提到的可能會發生漏算多算的原因。
這個精確度差距其實是可以給出一個估計值的:由正切差角公式,任兩個點的角度差為:
$$\tan\left(\arctan\left(\frac{p}{q}\right)-\arctan\left(\frac{r}{s}\right)\right)=\frac{ps-qr}{pr+qs}$$
由於整點座標 \(p, q, r, s\) 不超過 105,這個值的分子絕對值最小是 1,分母則不超過 \(2\times105^2=22050\),因此這個正切值若是非零則不小於 \(\frac1{22050}\approx4.535\times10^{-5}\),由正切的小角度近似也就知道角度值的差也大約至少有差這麼多。所以其實有個比較懶人的解法就是用老招術:取個比這個小許多的誤差值當相等。但一來到底要取多少才對只能用猜的,二來這無助於簡化「找對面」這回事,因為仍然需要檢查找到的對面旁邊有沒有同方向的點。
不過,至少在這個問題上,我們是有一個完全沒有浮點數誤差的做法的:直接比對兩個整點的方向位置。同樣利用上面那條公式,只要兩個方向不差超過 180 度,那我們就能用正切值分子 \(ps-qr\) 的正負 (或者等價地,其正弦值的正負) 來判斷兩個方向誰先誰後。不差超過 180 度的則可以簡單的決定一個對切 (例如沿 x 軸切開),不同邊的直接給答案,同一邊的再來代這個公式。這樣就能保持方向的整點座標而將它們排序了。
保持方向的整點座標還有一個好處是:我們可以動點手腳讓找對面這回事是 \(O(1)\)。有畫出圖的人都會注意到,同一個方向上的整點總是會一起參與計數:如果有個三角形有包住圓心,那把頂點在同一個方向上移動也仍然會包得到。因此,我們可以做一點小整理,把所有同方向的點給集合在一起,枚舉 A B 時就一口氣枚舉這個方向上的所有點一起計算。這樣一來,「對面」這個目標變單一了,而如果能夠利用一些資料結構,我們甚至可以在整理的時候就把「對面」關係給建立起來1,之後要找的時候直接沿著關係找過去就行了。這個操作並不會減少時間複雜度,因為所排序的點只是從所有數對變成所有互質數對,而大範圍內任取兩整數互質的機率是 \(\frac6{\pi^2}\approx60.8\%\) 是個常數,也就是我們只是把排序的點數減少為 60% 而已,仍然有 \(O(r^2)\) 個紀錄,因此這部份的時間複雜度是不會改變的,但多了處理上的方便性。
那麼找出範圍內的點數在有了這個整理之後,只要再花費 \(O(r^2)\) 掃一次做部份和,之後每次枚舉 A B 時 \(O(1)\) 找出對面邊界,部份和相減即可求出 C 點個數,乘起來加到總和即可。總計時間就是枚舉的 \(O(r^4)\),數秒內就能跑出答案來。實際程式的細節在這裡沒有提的還有很多,就不一一提了,順便當做一個有點故意的防抄 XD (這些細節只要有了上面的大概念,在實作中都會注意到的)
註腳
- 這一點由於比較細節就不詳提了,大略是利用了
std::map的實作,在進行方向統計時同時獲得對面方向的資料所在,而且這個所在不會因為後續新增資料而變動。 ↩︎