先提結果:因為一個做完題目後的決策失誤,今年又在 R2 落馬了。
意外的這場的難度並沒有很高;如果是平常就有在準備程式設計競賽的人應該可以輕鬆滿分吧。前三題我的時間是約一小時出頭,第四題有想出正確演算法的話一個半小時可以是綽綽有餘的--但 (ry
分數截圖以下有雷。

Q1. Minimum Sort
四題全部簡單看過一遍之後回頭就發現有人第一題 AC 了,想說第一題就互動題是不是有什麼鬼可以搞所以再仔細看了一下;之後在 Mathematica 求了這一個值之後就知道好的,果然被耍了:
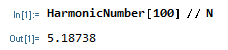
這個值顯著地小於 6 所以最直接的問法就行了。
Q2. Matrygons
很容易發現正多邊形邊數之間的因數關係,把這個因數關係寫下來就會是:輸入值 N 要找正整數 \((a_1,a_2,\dots,a_k)\),滿足 \(a_1\geq3,a_2,a_3,\cdots,a_k\geq2\),使得有 $$N=a_1+a_1 a_2+a_1 a_2 a_3+\cdots+a_1 a_2\cdots a_k=a_1(1+a_2(1+a_3(\cdots a_{k-1}(1+a_k)\cdots)))$$ 輸出就是最大的 k 值。
上面式子的套娃式結構 (繼續套用題目的比方 XD) 很自然的就能得到 DP 結構;不過問題在 \(a_1\geq3\) 的限制。如果它能是 2 的話那 DP 式就很單純,拆出所有因數後去看看 \(a_1\) 取誰能夠得到最大層數,加 1 指定進來就好。好在這問題容易解決:在 DP 時先做 \(a_1\geq3\) 的答案,抄去另一個陣列記起來之後再把 \(a_1=2\) 的狀況算完就好。
Q3. Hidden Pancakes
把給定數字能推得的大小關係畫出來之後容易看得出來它們形成了 n 個數的有向無圈樹,而所求即是這個樹的拓撲排序種類數。一般的有向無圈圖 (DAG) 的拓撲排序數問題其實是 #P-complete,不是容易能做的題目;不過這一題的結構額外還會形成一棵樹,而組合數問題中沒有限制通常代表更好算;一個點指向的各「子樹」之間沒有連結關係,所以可以各自求出組合數之後合併起來。公式很容易寫:遞迴地求出各別子樹組合數乘起來後,再乘上將所有點分給所有子樹的組合數,即是這個樹的組合數了。
這裡就是我文首提到的決策錯誤了:由於原題要求模 109+7 的關係,求分堆的組合數用到的除法會需要使用延伸歐基里德演算法求算模 109+7 的乘法反元素。原本我沒多想直接在每次要求時就算一次,想說應該還好的所以在看到小測資過之後就去做 Q4 了,賽後才發現隱藏的大測資是 TLE--而在多花了約十分鐘把階乘和階乘倒數模 109+7 建表之後就順利通過了。上面截圖可以看到這題送出的時間才只是開賽一小時而已,也就是如果我當時決定去把這邊改起來的話,拿到這 21 分就能進到晉級圈了。
Q4. Retiling
這題會想提的原因其實單純只是紀錄一下有想到正解,只不過因為太久沒寫這種演算法的關係一小時半還是來不及把演算法給實作出來。正解可以去看官方的題解,我的思考過程幾乎就跟題解的敘述方式一樣了就不多在這裡提;只是原本有打算過放掉大測資先做小的,但這一題的小測資其實並沒有比較好做,在全部想過之後會發現小測資的作用只是當做找到大測資做法的橋而已,所以後來還是嘗試一口氣寫出來,只是初版寫完時間就快到了所以 (倒)
總結
嘛,也就不用為決策錯誤找理由了,失誤就是失誤。今年 GCJ 果然還是只能到這裡為止了。
就在這裡提一下好了:今年接下來的一兩個月我有一些計畫要開跑,這個原本是要等兩週後另一件事完成後才會正式開始的,不過最近的大事讓這另一件事應該可以不用處理了,所以會提前開跑。應該會有一些能在這裡發表的東西出來,就請期待吧。
下一場下週日晚上的 GKS Round C 再見。