這次是因為有別的事所以晚了一天才來整理的 Round E。
稍微提一下上次的事:原本我以為 Round D 的時間我有事了,但那兩個月事情有點變化,原本排在這天的事不見了;只不過因為一些其他的原因,Round D 最後仍然沒有參戰。
Round E 最後是 248 名, 做了 1 3 4 題。分數截圖以下有雷。

Q1. Shuffled Anagrams
我其實很快就想到到題解做的移位解,不過倒是沒有細想到 \(\lfloor\frac{N}{2}\rfloor\) 這個關鍵值,而是直接掃過一遍找出最多字母的是誰,移那麼多位。意思其實是一樣的啦,就我多做了無用功而已。
Q3. Palindromic Crossword
看過 Q2 後覺得這題有點討厭,所以先跳題到 Q3 來。
題解提到的等價類很快就觀察到了,只是我並沒有把等價類給建立起來,而是直接下去掃每個格子,如果它有字且它的對稱位置沒字就把字丟過去,然後遞迴。
例如範例輸入 2,一開始看到 r1c1 的 A 檢查它的對稱格 (r1c4 和 r4c1),發現 r1c4 是空的,所以填 r1c4 為 A,然後換 r1c4 繼續。
……只是在 \(N\times M\leq10^6\) 的這個大小我其實有點擔心遞迴會爆堆疊就是了。好在這個遞迴是個尾遞迴,手動改寫成迴圈式並沒有花太多時間。時間複雜度方面,一組對稱連線至多會被走兩次,而列出對稱格如題解說明跟盤面一樣是 \(O(N\times M)\),所以總時間仍然是 \(O(N\times M)\)。我是不太確定誰的常數會比較大就是了……
Q4. Increasing Sequence Card Game
……差點就被這題給擺了一道。
我推的遞迴關係式其實和題解不太一樣:令有 \(N\) 張卡,且比目前已選擇的卡小的的卡片有 \(k\) 張,則剩下這部份的期望張數是
$$V(N,k)=1+\sum_{i=0}^k\left(\frac{k!}{(k-i)!}\cdot\left(\sum_{m=0}^{N-k-1} V(N-i-1,k-i+m)\right)\bigg/\frac{n!}{(n-i-1)!}\right)$$
中間的和式是這樣的:設下一張大卡前有 \(i\) 張小卡,先選這 \(i\) 張;再設下一張大卡是剩下的 \(N-k\) 張大卡中第 \(m+1\) 小的,這樣剩下的狀況就是 \(N-i-1\) 張卡,當中小卡有 \(k-i+m\) 張。這樣的機率,前 \(i\) 張選法有 \(P(k,i)=\frac{k!}{(k-i)!}\) 種,而 \(N\) 張牌裡固定了 \(i+1\) 張牌的機率是 \(\frac{1}{P(N,i+1)}=1\big/\frac{n!}{(n-i-1)!}\)。把這些所有狀況加起來,再 +1 (即是那下一張大卡) 就是所求了。邊界條件是 \(V(N,N)=0\),不過試算了前幾個分數看著有點眼熟……

除了看起來結果只跟 \(N-k\) 有關之外,這個數列:\(1,\frac32,\frac{11}6,\frac{25}{12},\frac{137}{60}\) 是個非常眼熟的東西--果然一減就發現我的直覺沒錯了:這結果是調和數,也就是調和級數的部份和。所以這題答案就很簡單了:把維基百科上的調和數近似展開式抄進去就好了:
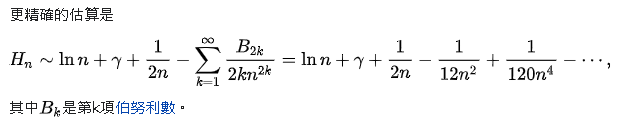
因為只在 \(n\) 很大時才代公式,\(n^4\) 足夠將精確度算到所要求的相對 \(10^{-6}\)。至於那個 +1……是因為預設輸出精確度是六位有效位數,不足以被判定為足夠近。加了個 setprecision(10) 就過了。
Q2. Birthday Cake
這題題目不難,但因為細節很多的關係不容易一次寫對,需要一點專注才行--而我當時就評估這題我要做的話會需要好好仔細細算一下各種輸入的邊界條件 (兩種意味上的,因為當要切下來的蛋糕在大蛋糕邊上時會有特殊狀況,麻煩的點就在這裡),所以就先跳過去做後面比較不那麼需要細節的兩題了。
也許是太急了吧,完全沒注意到當目標切下來之後裡面切成小塊必然會用掉恰好 \(NM-1\) 刀……詳細證明和切出目標的分析就請看題解吧。或許這題最後沒做出來其實是好事呢……
小結
這兩個月我有在開始嘗試一些其他東西 (Round D 沒有參戰有部份原因是這個),所以這篇離上篇才會離這麼久……不過不知道是不是又是惰性發作,嘗試的東西都沒能在時間到之前做完。這場比賽或許可以算是當做心情整理吧?之後再來看看吧。