簡單提一下 Round F 沒參戰的原因:因為它在半夜。上個月初因為一些事情回老家來,顯然不可能在有家人在的時候半夜起來寫 code……
這次成績是 108 名,只有 Q3 的大測資沒過。分數截圖以下有雷。

Q1. Dogs and Cats
總共最多只有一萬隻動物,所以就照題意餵過去就行了。不用太多處理。
Q4. Simple Polygon
然後就停住了。Q2 初看好像有點可怕所以跳過,Q3 好像要好一點的做法,Q4……有點不好湊的樣子。不過要求格子點這件事其實讓我想到皮克定理:簡單多邊形是皮克定理的前提,而題目給的目標是面積數值的兩倍,跟定理的形式也很合。
再仔細想想,皮克定理其實還告訴了我們到底要怎麼構造出要的形狀。怎麼說?如果,我們有辦法使構造出來的多邊形內部不含任何格點,那只要控制邊上的格點數就能做出任意 1/2 倍數的形狀了;稍微取一點巧,其至可以把邊上格點數全部放在同一邊,讓這一邊的另一頂點一路延伸出去。
稍微寫畫了一會之後,我找到了這個構造法:
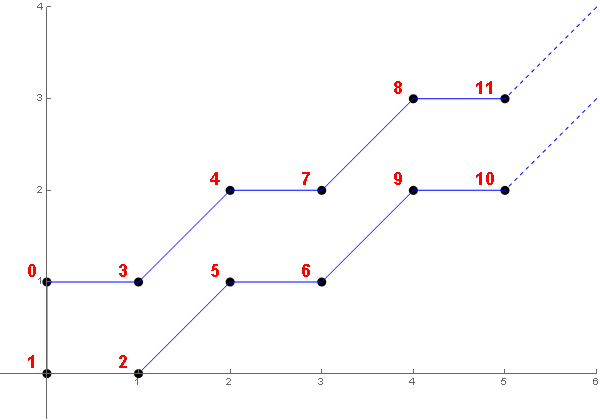
選取 0 到 N-1 號點,依照圖中的連法連成 N 邊形 (最後一邊是最右邊只有一個邊在圖上的兩點相連);如果面積要更大的話,則把 N-1 號點沿著圖中的邊的方向往外拉出去,每要多 1/2 面積就多拉到下一個格點。容易看到這個多邊形 (包含延伸出去的形狀) 內部不含格點,而延伸出去會把邊上的格點都放在同一邊 (拉出去的那個邊) 上,因此可以容易的確認這樣確實能構造出所要面積來。
無解的狀況呢?則還是回到皮克定理。N 邊形有 N 個頂點,所以邊界上的格點數至少是 N,因此面積至少是 N/2-1 (對應輸入值 N-2),因此比這個更小的輸入值就能判定為無解。
不過我的構造法稍微需要多一點點點的計算 (k 號點 x 座標是 \(\lfloor k/2\rfloor\),但 y 座標要從 \(\lfloor k/4\rfloor\) 上判定是餘 0 或 3 再加 1,然後延伸的方向對餘 0 餘 1 是右上,餘 2 餘 3 是右,也要做判斷);題解的構造法是一樣的道理,但取了更巧的擺法讓輸出座標幾乎沒有判斷式。
Q2. Staying Hydrated
這題我完全被它唬住了,因為看起來好像是一個很可怕的最佳化問題;不過仔細看下去才發現題目裡其實有好些個弱點存在。
第一個點就是:題目要最小化的是曼哈頓距離,不是歐氏距離。以一個用這種故事出的題目來說,求曼哈頓距離其實還滿怪的;仔細想就會發現,求曼哈頓距離的和代表其實我們可以把兩個座標軸拆開算。二維的題目變成了兩個一維題目,它要我們在數線上找一個點,使其對給定的許多區間的距離和最小。
好像還是很麻煩?我在思考到底要試算哪些點時才注意到:如果試算的點在兩個東西之間移動的話,對這兩個東西之間的距離和是固定的。這個性質其實馬上讓我聯想到一個題型的速解:形如 \(\sum_i\left|x-a_i\right|\) 式子的極小值發生在 x 值為所有 \(a_i\) 的中位數時。這個速解有個很幾何直覺的證明,而就是這個證明裡「x 值在座標軸上掃過去時的距離和的變化」讓我發現同樣的論證也能用在這個題目裡;差別只有在對單點時經過斜率會加 2,但對區間時這個加 2 會拆成兩個加 1 分別在兩端增加。因此,同樣的結論--極小值發生在中位數--對這個狀況也會成立。
所以答案就很簡單了:x y 座標各自收集起來,排序求中位數即可。由於座標數量一定是偶數,中位數一定是在兩個數之間;題目要求要給出座標最小的那個,所以答案就是這 2K 個數中第 K 小的那個。
Q3. Banana Bunches
最後這題……我卡在 \(O(N^4)\) 做法好一陣子,然後在寫 code 的過程之中才發現到可以寫 \(O(N^3)\),雖然覺得 5000 的三次方感覺有點微妙但就還是寫上去了。果然大測資吃了 TLE。
之所以沒考慮到更快的做法其實是被空間卡住了:簡單的記錄法好像會需要 \(O(NK)\) 的空間用來暫存東西及同樣的時間來計算,但 K 可以到一百萬,\(O(NK)\) 基本上沒救。這個的解決法就請參考題解了。
小結
從上面截圖可以看到,我把 1 4 2 三題做完的時間還不到一小時,而因為先做了第 4 題這個大分題,在那個當下我的分數 (67 分) 一度到了暫定第五名 (當時的前三名已破台,第四名則也是只剩 3 大測資的 86 分)。可惜一直沒能衝破 Q3 這個 \(O(NK)\) 的牆所以最終停在了這個位置。
Round H 是在中午,看看到時候我能不能參戰吧。