今年的 GKS 多了這個練習 Session,雖然不確定用意是什麼不過也算是個練習,於是雖然最近有點忙但還是抽了時間把題目做一做了。
那因為反正是練習 Session 所以就不貼成績了。繼續閱讀開始有雷。
Continue reading “GKS 2022 Practice Round 1”程式與遊戲的實驗室
今年的 GKS 多了這個練習 Session,雖然不確定用意是什麼不過也算是個練習,於是雖然最近有點忙但還是抽了時間把題目做一做了。
那因為反正是練習 Session 所以就不貼成績了。繼續閱讀開始有雷。
Continue reading “GKS 2022 Practice Round 1”因為各種原因,今天是在老家裡參戰,那 11am ~ 2pm 這段時間硬是卡了一個午飯時間就有點微妙了。還好中餐沒有耽誤到多少 (正好拿來讓我想題目),所以參戰結果還算滿意。
這次成績是 95 名,三四兩題的大測資都 TLE;不過這兩題看起來就是這場的魔王了,所以雖然只拿 62 分,但名次還有在前百。分數截圖以下有雷。

簡單提一下 Round F 沒參戰的原因:因為它在半夜。上個月初因為一些事情回老家來,顯然不可能在有家人在的時候半夜起來寫 code……
這次成績是 108 名,只有 Q3 的大測資沒過。分數截圖以下有雷。

又有一件「新聞」可以來順道談一些文字編碼的東西了。
這次的事件是這個:2021/9/22 數位五倍券開放登記當天,由於剛開啟時是人最多的時候,有不少人看到這樣的錯誤訊息:
甇斗�滚�嗵�⊥�蓥蝙�鍂��
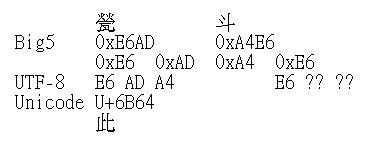
這是個很標準的編碼錯誤,而由大約一半的字是�來看,這有可能是 UTF-8 被當成 DBCS 編碼造成的。查了一下編碼表,容易發現前兩個字可以湊出東西來:
這次是因為有別的事所以晚了一天才來整理的 Round E。
稍微提一下上次的事:原本我以為 Round D 的時間我有事了,但那兩個月事情有點變化,原本排在這天的事不見了;只不過因為一些其他的原因,Round D 最後仍然沒有參戰。
Round E 最後是 248 名, 做了 1 3 4 題。分數截圖以下有雷。

嗯,這個週末跑去參加了 GMTK Game Jam 了。
Continue reading “GMTK Game Jam 2021 Entry”最近睡眠時間有點囧,晚上起來的時間讓開賽時腦袋還是一半睡著的狀態所以出了好些個簡單失誤吃了不少 attempt…還好這是 GKS 所以影響並不大就是了。
最終結果是做完前三題,第四題在賽後也花了另外的三個半小時寫完了。
分數截圖以下開始有雷。

先提結果:因為一個做完題目後的決策失誤,今年又在 R2 落馬了。
意外的這場的難度並沒有很高;如果是平常就有在準備程式設計競賽的人應該可以輕鬆滿分吧。前三題我的時間是約一小時出頭,第四題有想出正確演算法的話一個半小時可以是綽綽有餘的--但 (ry
分數截圖以下有雷。

這題題目描述起來很簡單:考慮平面上一些點的集合,這些點滿足:點的座標為整數,以及它們都在一個圓心在原點,半徑為 r 的圓的內部。考慮由這點集當中的點為頂點的三角形,計算圓心 (原點) 在其內部的三角形個數。
對 r=2,一共可以找得到 8 個原點在內部的三角形;r=3 有 360 個,而 r=5 則有 10600 個。試求 r=105 時有多少個。
看起來很簡單,但仔細想下去就會發現很多細節藏在裡面:
先來提「包含」這件事好了;因為這題其實是個標準的計算幾何題目。所謂計算幾何,以不那麼精準的懶人包說法就是:把幾何問題座標化的解析算式用電腦程式計算的演算法。畢竟電腦要「看」一個幾何圖形只能用描述它的參數性質去看,一些只要圖畫出來對人來說很直接的判斷,電腦程式都需要進行一些運算才能判定;加上一些幾何上的簡單性質其實很容易出現無理數 (以最常見的直角三角形來說好了,畢氏定理求斜邊會有根號,而角度則就連有理數度都是少數),若沒有特別設計的話數值精確度也會是一個問題。
在計算幾何當中要求一個點是否包在簡單多邊形當中,常用的做法有幾個:
等等。
單單只運用這些方式就能輕鬆寫程式檢驗題目給的三個數字,但直上 r=105 時就會卡住了。這才是這題的困難點:點集內有 \(O(r^2)\) 個點,所以選三個點組成的三角形個數有 \(O(r^6)\) 個,全部試過一遍的時間會太久。

來把題號擺在標題上好了。原本不放的原因是打算一篇可以擠好幾個,不過後來想想會能寫筆記的都應該不是三言兩語能解決的東西的。
所謂 Ulam sequence 是指這樣的數列:給定開頭兩個正整數 a < b,每次都找大於最後一項的整數當中,能夠唯一地表示為之前數列當中的兩項和的數中最小的那一個。題目給的例子是最簡單的 a=1, b=2 所產生的數列 (OEIS A002858):1, 2, 3, 4, 6, 8, 11, ……。因為 5 = 1+4 = 2+3 有兩種兩項和表示法,所以不在數列中;因此 6 就在數列中了 (只有 2+4 一種)。令這樣的數列第 \(k\) 項記為 \(U(a,b)_k\)。
試求 \(\sum_{n=2}^{10} U(2,2n+1)_k\),其中 \(k=10^{11}\)。
一般化的 Ulam sequence 其實有很多很詭異的性質,例如單就上面提的 a=1, b=2 產生的數列來說:
等等。不過這些都無助於我們求出第 1011 項--這個項數實在是太後面了,漸近性質沒辦法精準點到特定的某一項來。
