今年的 GKS 多了這個練習 Session，雖然不確定用意是什麼不過也算是個練習，於是雖然最近有點忙但還是抽了時間把題目做一做了。
那因為反正是練習 Session 所以就不貼成績了。繼續閱讀開始有雷。
Continue reading “GKS 2022 Practice Round 1”彙整
bookmark_borderGKS 2021 Round H
因為各種原因，今天是在老家裡參戰，那 11am ~ 2pm 這段時間硬是卡了一個午飯時間就有點微妙了。還好中餐沒有耽誤到多少 (正好拿來讓我想題目)，所以參戰結果還算滿意。
這次成績是 95 名，三四兩題的大測資都 TLE；不過這兩題看起來就是這場的魔王了，所以雖然只拿 62 分，但名次還有在前百。分數截圖以下有雷。
bookmark_borderGKS 2021 Round G
簡單提一下 Round F 沒參戰的原因：因為它在半夜。上個月初因為一些事情回老家來，顯然不可能在有家人在的時候半夜起來寫 code……
這次成績是 108 名，只有 Q3 的大測資沒過。分數截圖以下有雷。
bookmark_border文字編碼雜談 (5)
又有一件「新聞」可以來順道談一些文字編碼的東西了。
這次的事件是這個：2021/9/22 數位五倍券開放登記當天，由於剛開啟時是人最多的時候，有不少人看到這樣的錯誤訊息：
甇斗�滚�嗵�⊥�蓥蝙�鍂��
這是個很標準的編碼錯誤，而由大約一半的字是�來看，這有可能是 UTF-8 被當成 DBCS 編碼造成的。查了一下編碼表，容易發現前兩個字可以湊出東西來：
bookmark_borderGKS 2021 Round E
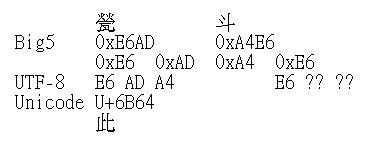
這次是因為有別的事所以晚了一天才來整理的 Round E。
稍微提一下上次的事：原本我以為 Round D 的時間我有事了，但那兩個月事情有點變化，原本排在這天的事不見了；只不過因為一些其他的原因，Round D 最後仍然沒有參戰。
Round E 最後是 248 名, 做了 1 3 4 題。分數截圖以下有雷。
bookmark_borderDoki Doki Literature Club Plus 新要素我流整理考察
DDLC 終於在睽違四年之後出了加強版 DDLC Plus 了。官方的宣傳是說除了本篇之外，還有六條兩兩成員之間的互動支線，以及會在其他平台上登場等等。所以這裡我想來做個我流的新要素整理及考察 (腦洞)。
為了做一點簡單的防雷，繼續閱讀之下會先放張 Monika，然後是一部份新要素整理 (主要面對有玩過 2017 原版的人，做一些比較沒有爆雷問題的新要素說明)，然後會有第二張 Monika，那之下才是隱藏要素的整理。要自己避雷的就自行斟酌看的內容吧。
噢還有，這篇所有的圖雖然都是我自己的截圖，但我全部都手動縮小成一半大小，這樣稍微省一點流量，順帶讓文字小一點做為再一重的微防雷 XD 要詳細內容的就自行進遊戲操作吧。
Continue reading “Doki Doki Literature Club Plus 新要素我流整理考察”bookmark_borderGMTK Game Jam 2021 Entry
嗯，這個週末跑去參加了 GMTK Game Jam 了。
Continue reading “GMTK Game Jam 2021 Entry”bookmark_borderGKS 2021 Round C
最近睡眠時間有點囧，晚上起來的時間讓開賽時腦袋還是一半睡著的狀態所以出了好些個簡單失誤吃了不少 attempt…還好這是 GKS 所以影響並不大就是了。
最終結果是做完前三題，第四題在賽後也花了另外的三個半小時寫完了。
分數截圖以下開始有雷。
bookmark_borderGCJ 2021 Round 2
先提結果：因為一個做完題目後的決策失誤，今年又在 R2 落馬了。
意外的這場的難度並沒有很高；如果是平常就有在準備程式設計競賽的人應該可以輕鬆滿分吧。前三題我的時間是約一小時出頭，第四題有想出正確演算法的話一個半小時可以是綽綽有餘的－－但 (ry
分數截圖以下有雷。
bookmark_borderProject Euler 解題筆記 (4) – #184
#184 Triangles containing the origin (難度 75%)
這題題目描述起來很簡單：考慮平面上一些點的集合，這些點滿足：點的座標為整數，以及它們都在一個圓心在原點，半徑為 r 的圓的內部。考慮由這點集當中的點為頂點的三角形，計算圓心 (原點) 在其內部的三角形個數。
對 r=2，一共可以找得到 8 個原點在內部的三角形；r=3 有 360 個，而 r=5 則有 10600 個。試求 r=105 時有多少個。
看起來很簡單，但仔細想下去就會發現很多細節藏在裡面：
- 首先，點的數量很多：用圓面積估計可以得到半徑 105 的圓內整點數約有三萬四千多個，在其中選三個的選法有近七兆種；
- 三角形要包含圓心。說起來簡單，但包含這回事並不容易化成條件；
- 看起來好像有一些對稱性可以用，但這又不是大家都一樣的對稱 (有的翻轉不同，有的翻轉相同等等)，要分狀況會很麻煩；
- 等等。
先來提「包含」這件事好了；因為這題其實是個標準的計算幾何題目。所謂計算幾何，以不那麼精準的懶人包說法就是：把幾何問題座標化的解析算式用電腦程式計算的演算法。畢竟電腦要「看」一個幾何圖形只能用描述它的參數性質去看，一些只要圖畫出來對人來說很直接的判斷，電腦程式都需要進行一些運算才能判定；加上一些幾何上的簡單性質其實很容易出現無理數 (以最常見的直角三角形來說好了，畢氏定理求斜邊會有根號，而角度則就連有理數度都是少數)，若沒有特別設計的話數值精確度也會是一個問題。
在計算幾何當中要求一個點是否包在簡單多邊形當中，常用的做法有幾個：
- 繞多邊形的邊，每次都看該點是否在邊的同一側：想像沿著多邊形開車，結果繞了一圈都發現目標點都在同一邊，那就可以知道這個點在多邊形裡面了。從這個形象化也很容易知道知道這個方法只對凸多邊形有用，不過三角形一定是凸的所以對三角形也算常用。
- 從點任意發射射線，如果只和多邊形交叉奇數次那就是在裡面：這也是個在圖形上滿直觀的做法。
- 上一個方法的進階版：計算這個多邊形對所求點的卷繞數，如果不是零那就是在裡面。
等等。
單單只運用這些方式就能輕鬆寫程式檢驗題目給的三個數字，但直上 r=105 時就會卡住了。這才是這題的困難點：點集內有 \(O(r^2)\) 個點，所以選三個點組成的三角形個數有 \(O(r^6)\) 個，全部試過一遍的時間會太久。
